Interactive Learning

Posted On:

Motivation

Most modern machine learning algorithms are all based on the same feature weighing framework, i.e. F(\mathbf{w}^\intercal \mathbf{x}). In order to capture the possible inter-relationship between features, the prevalent way is to expand the feature set \mathbf{x} by including interactive terms. However, this process is very ad-hoc, and it depends on a lot of manual trial-errors.

Proposal

In order to overcome the above plight, I propose a brand new learning framework F(\mathbf{x}) = \prod_{j=0}^{j=m} \left[ \sum_{k=0}^{d} a_{j, k} \cdot \left( x_j \right)^{k} \right], in which \sum_{k=0}^{d} a_{j, k} \cdot \left( x_j \right)^{k} represents the general polynomial form of one of the m features x_j up to d degrees. d is a hyperparameter that can be searched incrementally.

This framework provides a more intuitive learning strategy, which permits the model a much more power to fit the hypothetical relationship between given features.

Derivations of Gradients

Assuming that y \sim F(\mathbf{x}) and our goal is to minimize their L2 distances, we have our objective function as \mathcal{L} \coloneqq \argmin_{a_{j, k}} \left( F(\mathbf{x}) - y \right)^2. At the optimal, we know that it is equivalent to \argmin_{a_{j, k}} \left( \log F(\mathbf{x}) - \log y \right)^2 = \argmin_{a_{j, k}} \left\{ \sum_{j=0}^{m} \log \left[ \sum_{k=0}^{d} a_{j, k} \cdot \left( x_j \right)^{k} \right] - \log y \right\}^2.

Thus, its first-order derivative is \frac{\partial \mathcal{L}}{\partial a_{j, k}} = 2 \cdot \left\{ \sum_{j=0}^{m} \log \left[ \sum_{k=0}^{d} a_{j, k} \cdot \left( x_j \right)^{k} \right] - \log y \right\} \cdot \frac{\left( x_j \right)^{k}}{\sum_{k=0}^{d} a_{j, k} \cdot \left( x_j \right)^{k}}; while its second-order derivative is \frac{\partial^2 \mathcal{L}}{\partial a_{j, k} \partial a_{p, q}} = 2 \cdot \frac{\left( x_j \right)^{k} \cdot \left\{ 1 - \left\{ \sum_{j=0}^{m} \log \left[ \sum_{k=0}^{d} a_{j, k} \cdot \left( x_j \right)^{k} \right] - \log y \right\} \cdot \left( x_p \right)^{q} \right\}}{\left[ \sum_{k=0}^{d} a_{j, k} \cdot \left( x_j \right)^{k} \right]^2}.

Unresolved Challenges

  1. To make the above derivations, two strong assumptions have to be satisfied: 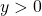y > 0 and \sum_{k=0}^{d} a_{j, k} \cdot \left( x_j \right)^{k} > 0,\ \forall j.
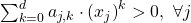  2. In order to speed up the convergence speed, it is better to use the Newton Method to decide the step size, which requires the Jacobian matrix made of 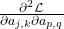\frac{\partial^2 \mathcal{L}}{\partial a_{j, k} \partial a_{p, q}} to be positive definite instead of positive semi-definite.
  3. To improve the calculation precision of floating numbers, it will be more ideal to calculate 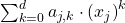\sum_{k=0}^{d} a_{j, k} \cdot \left( x_j \right)^{k} in log space then convert the result back to normal space. However, to do so, we need to again make sure 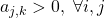a_{j, k} > 0,\ \forall i, j and x_j > 0,\ \forall j.

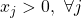Workarounds

I tried to move the calculation from real number domain to complex number domain, whose calculation are supported by most of the Python libraries. However, I am not sure what each number implies in a complex number domain. What’s worse, sometimes the model’s convergence is still pretty bad.

Attachments

Github Link

Keywords

Interactive Learning

Leave a Reply

Your email address will not be published. Required fields are marked *